Introduction
Une série de 32 images CCD ont été prises avec la caméra CCD du Club Astro Tarbais dans la nuit du 13 au 14 décembre 1992 entre 1h35 et 1h49 TU à l’observatoire du Pic du Midi. La caméra (matrice Thomson 7852, 145 x 221 pixels) était montée au foyer du T60 en configuration Newton (2100 mm de focale, 600 mm de diamètre).
Le but de l’étude présentée ici est de déterminer la distance angulaire entre Toutatis et l’étoile SAO117887 lors de la conjonction. En effet, un calcul du Bureau des Longitudes et de Jean Lecacheux de l’Observatoire de Meudon prévoyait une séparation angulaire minimale entre les deux astres de 32" d’arc à 1h41,9 TU le 14 décembre 1992.
La valeur de 32" d’arc a été calculée en faisant l’intégration numérique pas à pas de la trajectoire de Toutatis, avec comme conditions initiales les éléments osculateurs pour le 13.0 janvier 1993 prédits dès novembre 1992 par D.K.Yeomans du Jet Propulsion Laboratory (Yeomans a analysé toutes les observations connues entre la pré-découverte de 1934 et septembre 1992). De plus, la valeur de 32" inclut la correction de parallaxe due aux coordonnées géographiques et à l’altitude du Pic du Midi.
Présentation du problème
Pour toutes les images, le temps de pose était de 10 secondes. La figure ci-dessous schématise l’étoile SAO ainsi que les deux positions extrêmes de Toutatis relevées durant les prises de vues :
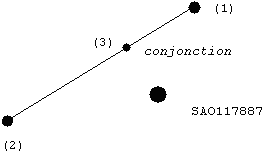
position (1) : Toutatis observé à 1h35m29s
position (2) : Toutatis observé à 1h49m46s
position (3) : position de Toutatis à la conjonction
L’étoile SAO117887 (aussi dénommée PPM156319) a les coordonnées équatoriales suivantes :

Il s’agit d’une étoile variable de type M (rouge). Elle est connue sous la dénomination RR Sextant et sa magnitude varie grossièrement entre 9 et 10,5.
Les heures de prise de vues vont nous permettre de déterminer grossièrement l’instant de la conjonction. De plus, la calibration de l’image à partir des deux positions extrêmes de Toutatis et d’un éphéméride va nous permettre de déterminer la distance angulaire entre Toutatis et l’étoile SAO à cet instant.
Analyse des clichés
L’analyse de la première et de la 32ème et dernière vues donne les côtes relatives suivantes, exprimées en pixels dans le repère de la première image :
position (1) : X = 68,548, Y = 89,081
position (2) : X = 37,274, Y = 140,161
étoile SAO117887 : X = 45,937, Y = 104,367
Ces côtes sont obtenues directement à l’écran à l’aide d’une fonction de détermination du centre d’un objet brillant proposée par le logiciel ASTROL, logiciel développé par François Colas du Bureau de Longitudes.
De la même façon, une analyse des images autour du point de conjonction donne les valeurs suivantes (les côtes sont exprimées dans le repère particulier à chaque image, mais il reste possible de comparer directement les distances relevées entre Toutatis et l’étoile SAO) :

La figure suivante montre la courbe que l’on obtient si l’on reporte les distances (colonne d) en fonction du temps (exprimé en secondes depuis l’instant 1:40:00) :

Un calcul simple permet de déterminer la courbe d’équation
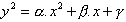
qui passe par trois des six points de la figure. En effet, c’est une courbe de ce type qui décrit la distance en fonction du temps dans le cas où l’on fait l’hypothèse que Toutatis possède une vitesse constante sur une trajectoire rectiligne durant l’intervalle de temps qui nous intéresse. On vérifie que les trois autres points ne s’écartent pas de la courbe de manière significative.
On trouve alors les valeurs suivantes pour les paramètres de l’équation :
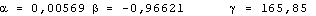
Détermination de l’instant de la conjonction
En dérivant l’équation obtenue dans le paragraphe précédent, on trouve que le sommet de la courbe a pour abscisse 85,0 secondes et pour ordonnée 11,17 pixels. On en déduit facilement l’instant de la conjonction :
passage au point (3) : 1h41m25s
La prévision du Bureau des Longitudes et de l’Observatoire de Meudon donne l’instant 1h41m54s.
La différence peut être au moins partiellement expliquée par le fait que la datation des clichés est approximative. En effet, le logiciel d’acquisition enregistre l’heure de sauvegarde du fichier et non l’heure du début ou de fin de pose (chaque pose durant 10 secondes). De plus, on peut raisonnablement supposer que l’horloge interne du système était synchronisée sur l’heure TU à quelques secondes près. Tout cela fait que le résultat obtenu peut être considéré comme satisfaisant.
Détermination de la distance angulaire
Un éphéméride de Toutatis fourni par Jean Lecacheux (cet éphéméride a été préparé par Patrick Rocher du Bureau des Longitudes à l’aide d’un programme d’intégration numérique) donne la position de Toutatis toutes les dix minutes dans la plage horaire qui nous intéresse (pour le site de l’Observatoire du Pic du Midi) :

La calibration du cliché en orientation et échelle peut être réalisée à l’aide de cet éphéméride pour peu que l’on ait une précision suffisante au niveau du relevé des temps pour chacun des clichés. Cette condition n’est pas entièrement réalisée puisque l’on prend en compte l’heure de sauvegarde du fichier par le logiciel d’acquisition d’images. On fera toutefois l’hypothèse que cette précision est suffisante pour le calcul que nous voulons réaliser.
Un cliché de Schmidt calibré avec le PPM de la portion de ciel qui nous intéresse permettrait bien sûr de ne plus faire reposer notre calibration sur le vecteur vitesse de Toutatis et donc d’augmenter la précision de notre détermination de distance angulaire. Il se peut qu’un tel cliché soit disponible dans les mois à venir, auquel cas un nouveau calcul sera entrepris.
A partir de l’éphéméride, on détermine par interpolation que la distance angulaire entre les points (1) et (2) est de 167,23" d’arc. Dans notre système de coordonnées relatives, la distance qui sépare le point (1) du point (2) est de 58,83 pixels.
Dans le paragraphe précédent, nous avons déterminé que la distance qui sépare l’étoile SAO du point (3) est de 11,17 pixels.
On en déduit par une simple règle de trois que la distance angulaire entre l’étoile SAO et le point (3) est de 31,8" d’arc environ. La prévision du Bureau des Longitudes et de l’Observatoire de Meudon donne une distance angulaire de 32" d’arc.
Conclusion
Avec le champ fourni par l’instrument, un pixel de l’image représente environ 2,84" d’arc. L’analyse des différentes imprécisions (obtenues en particulier en déterminant la distance en pixels entre deux étoiles fixes sur plusieurs images) montre que l’on peut s’attendre à une erreur d’environ +/- 0,2 pixels sur le relevé des positions, ce qui induit donc une incertitude d’environ +/- 0,5" d’arc sur la distance angulaire au moment de la conjonction.
En conclusion, on pouvait légitimement s’attendre à trouver une différence de plusieurs secondes d’arc entre la position calculée et la position observée de Toutatis. Le fait de trouver la même valeur (aux incertitudes près) constitue donc une résultat intéressant qui montre que les astronomes de l’Observatoire de Meudon et du Bureau des Longitudes ont maintenant une bonne connaissance de la trajectoire de Toutatis.
Sur la base des mêmes éléments orbitaux qui ont servi au calcul de l’éphéméride présenté dans cette étude, les astronomes ont prédit un passage de Toutatis au plus près de la Terre le 29 septembre 2004 à environ 13h37 TU. Cette prévision fait bien sûr l’hypothèse que l’astéroïde ne verra pas sa trajectoire modifiée en réaction à un dégazage imprévisible.
A cette date, Toutatis sera approximativement à 1,55 million de kilomètres de la Terre, ce qui infirme de façon certaine les prévisions pessimistes (collision entre la Terre et Toutatis) qui ont fait la une des journaux il y a quelques semaines !
Remerciements
Les auteurs tiennent à remercier Jean Lecacheux de l’Observatoire de Meudon et François Colas du Bureau des Longitudes pour l’aide qu’ils leur ont apportés dans la réalisation de ce travail.
